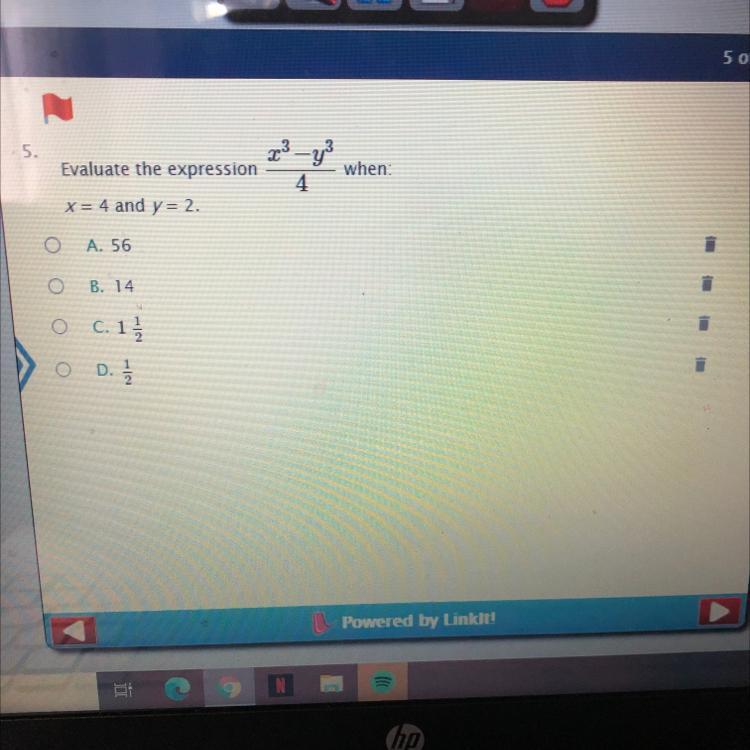
Answers
Answer:
Option B is correct
Step-by-step explanation:
[tex] \sf \longmapsto \: \frac{{x}^{3} - {y}^{3} }{4} \\ \sf \longmapsto \: \frac{ {4}^{3} - {2}^{3} }{4} \\ \sf \longmapsto \: \frac{64 - 8}{4} \\ \sf \longmapsto \: \frac{56}{4} \: \: \: \: \: \: \: \: \\ \sf \longmapsto \: 14[/tex]
Related Questions
Which expression is equivalent to7sqrt x^2/ 5 sqrt y^3
?Assume y/=0,
Answers
Answer:
7sq rt = 2.6457513110645907 = sqrt y^3
Step-by-step explanation:
i need to know what this movie is, what is the name of this move.
Answers
Answer:
Step-by-step explanation:
Percy Jakcson maybe?
THIS QUESTION IS WORTH 50 POINTSMatt and his friends hike 42 mi over a holiday weekend. they hike for 5 hours on saturday, 6 hours on sunday, and 3 hours on monday. they go hiking the following weekend. if they hike at the same rate as they hiked over the holiday weekend, how long will it take to hike 12 mi
Answers
Una persona compra borregos, cabras y puercos jabalí. Son 100 animales vivos en total y paga $100 mil pesos. Cada borrego costó $500 pesos, tres cabras cuestan $4000 y cada puerco jabalí $3500.
Si denotamos con la variable xel número de borregos comprados por la persona, con y el número de cabras y con z el número de puercos jabalí, escribe las ecuaciones que representan las relaciones entre x,y,zde acuerdo a la información proporcionada.
Answers
Answer:
I'm sorry I just need points
Step-by-step explanation:
what is 5 1/2 + 2 1/7
Answers
Answer:
[tex]7\frac{9}{14}[/tex]
Step-by-step explanation:
5 1/ 2 +2 1/ 7
= 11/ 2 +2 1/ 7
= 11/ 2 + 15/ 7
= 107/ 14
=7 9/ 14
Answer:
7 9/14
Step-by-step explanation:
Combine the whole numbers and fractions together:
(5 + 2) + ( 1/2 + 1/7)
The whole numbers part is:
5 + 2 = 7
For the fractions part:
The Least Common Multiple (LCM) of 2 and 7 is 14. Multiply the numerator and denominator of each fraction by whatever value will result in the denominator of each fraction being equal to the LCM:
1/2 + 1/7 = 1 × 7 + 1 × 2
--------- ------- = 7 /14 + 2/14 = 7 9/14
2 × 7 + 7 × 2
Which graph represents an odd function?
please hurry its timed
Answers
Considering it's definition, an odd function is represented by the second function given.
What defines an odd function?An odd function is defined by the following rule:
f(x) = -f(x).
This means that for example:
If f(1) = -1, then f(-1) = 1.If f(2) = 0, then f(-2) = 0.If f(3) = 5, then f(-3) = -5.The only graph for which this relation is valid in this problem is the second graph, from which all examples off the numeric values were taken, hence an odd function is represented by the second function given.
More can be learned about odd functions at https://brainly.com/question/2284364
#SPJ1
For every 1000 videos a channel gets it makes £2.50 from ad revenue. How many videos will the channel need to make £1
Answers
Answer: 400 videos
Step-by-step explanation:
1000/1 x 1/2.5 = 400
Solve the rational equation:
1 1 1
x-2x+3 5
O A. X=-6.09, x= 5.09
B. There is no solution.
O C. x=-3.09, x= 2.09
D. X=-3, x= 2
Answers
………………. ……………
The solutions for the equation 23 - x² - 2x = 0 are:
x = 4
x = -6
Option A is the correct answer.
We have,
To solve the rational equation:
1/(x - 1) - 1/(x + 3) - 1/5 = 0
We need to find the common denominator and combine the fractions on the left-hand side.
The common denominator is (x - 1)(x + 3)(5).
Multiplying each term by the common denominator:
[(x + 3)(5) - (x - 1)(5) - (x - 1)(x + 3)] / [(x - 1)(x + 3)(5)] = 0
Simplifying:
[5(x + 3) - 5(x - 1) - (x - 1)(x + 3)] / [(x - 1)(x + 3)(5)] = 0
[5x + 15 - 5x + 5 - (x² + 3x - x - 3)] / [(x - 1)(x + 3)(5)] = 0
[5x + 15 - 5x + 5 - x² - 3x + x + 3 ] / [(x - 1)(x + 3)(5)] = 0
Simplifying further:
[23 - x² - 2x ] / [(x - 1)(x + 3)(5)] = 0
Now, we set the numerator equal to zero since a fraction is zero if and only if its numerator is zero:
23 - x² - 2x = 0
To solve the quadratic equation 23 - x² - 2x = 0, we can rearrange it to the standard form:
x² + 2x - 23 = 0
Now, we can solve it using factoring, completing the square, or the quadratic formula. Let's solve it using the quadratic formula:
The quadratic formula states that for an equation in the form
ax² + bx + c = 0, the solutions for x are given by:
x = (-b ± √(b² - 4ac)) / (2a)
For our equation x² + 2x - 23 = 0, the coefficients are a = 1, b = 2, and
c = -23.
Substituting these values into the quadratic formula:
x = (-2 ± √(2² - 4(1)(-23))) / (2(1))
Simplifying:
x = (-2 ± √(4 + 92)) / 2
x = (-2 ± √96) / 2
x = (-2 ± 4√6) / 2
Simplifying further:
x = -1 ± 2√6
Therefore,
The solutions for the equation 23 - x² - 2x = 0 are:
x = -1 + 2√6 = 3.89 = 4
x = -1 - 2√6 = -5.89 = -6
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ6
Slope = 4
Y-intercept = -1
Answers
Answer:
y = 4x -1
Step-by-step explanation:
You use the equation y = mx + b
m is the slope, so you just substitute 4 for m, and b is the y-intercept, so you substitute -1 for b
A: $521.80
B:513.60
C: 467.90
D: 435.70
Answers
Answer:
I think it´s A $521.80
Step-by-step explanation:
It’s A hopeful you got it right
A study was conducted and two types of engines, A and B, were compared. Fifty experiments were performed using engine A and 75 using B. The average gas mileage for A was 36 mpg, and 42 mpg for B. Assume population standard deviations for A and B are respectively 6 and 8. A. Find the point estimate. (2 pts) B. Find the margin of error. (3 pts) C. Construct the 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results(5 pts)
Answers
Answer:
a) -6 mpg.
b) 2.77 mpg
c) The 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results, in mpg, is (-8.77, -3.23).
Step-by-step explanation:
To solve this question, we need to understand the central limit theorem, and subtraction of normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean [tex]\mu[/tex] and standard deviation [tex]s = \frac{\sigma}{\sqrt{n}}[/tex].
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean [tex]\mu = p[/tex] and standard deviation [tex]s = \sqrt{\frac{p(1-p)}{n}}[/tex]
Subtraction between normal variables:
When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.
Gas mileage A: Mean 36, standard deviation 6, sample of 50:
So
[tex]\mu_A = 36, s_A = \frac{6}{\sqrt{50}} = 0.8485[/tex]
Gas mileage B: Mean 42, standard deviation 8, sample of 50:
So
[tex]\mu_B = 42, s_B = \frac{8}{\sqrt{50}} = 1.1314[/tex]
Distribution of the difference:
Mean:
[tex]\mu = \mu_A - \mu_B = 36 - 42 = -6[/tex]
Standard error:
[tex]s = \sqrt{s_A^2+s_B^2} = \sqrt{0.8485^2+1.1314^2} = 1.4142[/tex]
A. Find the point estimate.
This is the difference of means, that is, -6 mpg.
B. Find the margin of error
We have that to find our [tex]\alpha[/tex] level, that is the subtraction of 1 by the confidence interval divided by 2. So:
[tex]\alpha = \frac{1 - 0.95}{2} = 0.025[/tex]
Now, we have to find z in the Ztable as such z has a pvalue of [tex]1 - \alpha[/tex].
That is z with a pvalue of [tex]1 - 0.025 = 0.975[/tex], so Z = 1.96.
Now, find the margin of error M as such
[tex]M = zs = 1.96*1.4142 = 2.77[/tex]
The margin of error is of 2.77 mpg
C. Construct the 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results(5 pts)
The lower end of the interval is the sample mean subtracted by M. So it is -6 - 2.77 = -8.77 mpg
The upper end of the interval is the sample mean added to M. So it is -6 + 2.77 = -3.23 mpg
The 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results, in mpg, is (-8.77, -3.23).
Alex has 5 1/5cups of dog food. A serving of dog food is 4/5cup.
How many servings does Alex have?
O A.
8
55
serving
B. 4; servings
O c. 5 servings
OD.
D. 67 servings
Answers
5 servings looked It up
Alex has 5 1/5cups of dog food. A serving of dog food is 4/5cup. Therefore, Alex has 4 servings.
What is the unitary method?The unitary method is a method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value.
Alex has 5 1/5 cups of dog food. A serving of dog food is 4/5 cup.
[tex]5\dfrac{1}{5} = \dfrac{26}{5}\\\\= \dfrac{26}{5}/ \dfrac{4}{5} \\\\= \dfrac{26}{5}\times \dfrac{5}{4} \\\\=\dfrac{26}{4}[/tex]
Therefore, Alex has 4 servings.
Learn more about the unitary method;
https://brainly.com/question/23423168
#SPJ2
Add the fraction : 3/5 + 5 2/5 + 1/6
Answers
Answer:
37/6 or 6 1/6
Step-by-step explanation:
make all the denominators the same and add the numerators
-4, 1, 8, 4, 8, 7, 10, -5, -2, 7
Work out the mean temperature
Please help me the homework is due tomorrow
Answers
(no links) Please Help!
Answers
Answer:
Part A: D Part B: B
Step-by-step explanation:
This question is so free
Can someone help me with this?
Answers
Answer:
add to 180, equal, add to 180, equal
Step-by-step explanation:
<1 + <2 = 180
<1 = <3
<3 + <4 = 180
<2 = <4
determine a if x-2 is a factor of f(x)=x^4-3x^3+ax^2-16x+20
Answers
Answer:
x-2 is factor so 2 is zero of f(x) =x^4-3x^3+ax^2-16x+20
Step-by-step explanation:
2^4-3×2^3+a×2^2-16×2+20
solve this Answer is come.THANK YOU.
If (x - 2) is a factor of the polynomial f(x) = x⁴ -3x³ + ax² -16x + 20.
Then the value of a is -17.
What is a polynomial?An expression that consists of variables, constants, and exponents that are combined using mathematical operations like addition, subtraction, multiplication, and division is referred to as a polynomial.
Given:
A polynomial,
x⁴ -3x³ + ax² -16x + 20.
If x - 2 is a factor the x = 2 is the zeros of the polynomial.
When x = 2,
then,
x⁴ -3x³ + ax² -16x + 20 = 0
2⁴ -3(2)³ + a(2)² -16(2) + 20 =0
48 + 20 + 4a = 0
4a = -68
a = -17
Therefore, the value of a is -17.
To learn more about the Polynomials;
brainly.com/question/11536910
#SPJ2
find 5 consecutive odd numbers where the sum of the first three numbers is 15 greater than the sum of two numbers
Answers
Answer:
The five odd numbers are:
23, 25, 27, 29, and 31
Step-by-step explanation:
A random odd number is written as:
2*n + 1
Where n is an integer.
Then 5 consecutive odd numbers will be:
2*n + 1
2*(n + 1) + 1
2*(n + 2) + 1
2*(n + 3) + 1
2*(n + 4) + 1
Now we want that the sum of the first 3 numbers to be 15 greater than the sum of the two last numbers, then:
(2*n + 1) + (2*(n + 1) + 1) + (2*(n + 2) + 1) = 15 + (2*(n + 3) + 1) + (2*(n + 4) + 1)
Now we just need to solve this for n:
(2*n + 1) + (2*n + 3) + (2*n + 5) = 15 + (2*n + 7) + (2*n + 9)
6*n + 9 = (15 + 7 + 9) + 4*n
6*n - 4*n = 15 + 7 + 9 - 9
2*n = 15 + 7 = 22
n = 22/2 = 11
Then the five numbers are:
(2*11 + 1) = 23
(2*(11 + 1) + 1) = 25
(2*(11 + 2) + 1) = 27
(2*(11 + 3) + 1) = 29
(2*(11 + 4) + 1) = 31
what is the value of n?
Answers
Answer:
5?
Step-by-step explanation:
What is the volume of the following rectangular prism? 8 units 5 1/4 units2
Answers
Answer:
84 units²
Step-by-step explanation:
v = 8 * 5 1/4 * 2
v = 84 units²
The volume of the rectangular prism is 42 cubic units.
What is volume?Volume is defined as the mass of the object per unit density while for geometry it is calculated as profile area multiplied by the length at which that profile is extruded.
To find the volume of a rectangular prism, you need to multiply the height of the prism by the base area.
The height of the prism is given as 8 units.
The base area is given as 5 1/4 units².
To convert the mixed fraction to an improper fraction, we multiply the whole number (5) by the denominator (4), then add the numerator (1).
5 1/4 = (5 x 4 + 1) / 4 = 21/4
Now, we can calculate the volume of the rectangular prism:
Volume = height x base area
Volume = 8 x 21/4
Volume = 168/4
Volume = 42
Therefore, the volume of the rectangular prism is 42 cubic units.
Learn more about Volume here:
https://brainly.com/question/1578538
#SPJ2
help please please help
Answers
Answer:
2/10 (A)
Step-by-step explanation:
explain why you rename 4 1/4 to find 4 1/4- 3/4
Answers
Answer:
Because it is a mixed fraction and it should be renamed in order to solve your problem, for the other one CAN NOT be converted into a mixed fraction.
It would be nice if someone helped!
Thank you I’m advanced
Answers
Answer: 243 inches squared.
Step-by-step explanation: I could be wrong but here's my answer
[tex]\int\{-2+(x^{2} +3x)^(6/5) - x^3} \, dx[/tex]
Answers
Apply sum rule:
- 2dx + (x^2 +3x) 6/5dx = x^3dx
2dx = 2x
(x^2 + 3x) 6/5dx = 6/5 (x^3/3 + 3x^2/2)
x^3dx = x^4/4
-2x + 6/5 (x^3/3 + 3x^2/2) - x^4/4
Add constant
-2x + 6/5 (x^3/3 + 3x^2/2) - x^4/4 + c
What is the length of the diagonal of a non -regulation tennis court with length 20 feet and width 15 feet
Answers
Answer:
25 feet
Step-by-step explanation:
using the sides 20 and 15, use the Pythagorean theorem to find the hypotenuse of the right triangle formed by the 2 side lengths and the diagonal.
[tex]a^{2} +b^{2} =c^{2} \\20^{2} +15^{2} =c^{2} \\400+225=c^{2} \\625=c^{2} \\25=c[/tex]
O2) Work out 30% of £5.80.
Answers
Answer:
1.74
Step-by-step explanation:
Multiply 5.80 times .30
Answer:
1.74
Step-by-step explanation:
To solve this, lets multiply the value by the percentage.
Our value is 5.8
And our percentage is 30%.
Lets convert this into a decimal, to do this, divide 30 by 100:
30/100
=
0.3
Now that we have the percentage in decimal form, multiply it by the 5.8:
5.8*0.3
=
1.74
This is your answer!
Hope this helps! :)
Pls help!!
Jody has 15 pound bag of potatoes. She uses 3/4 of the bag to make potato salad. How many pounds of potatoes does Jody use for the potato salad?
Answers
Answer:
11.25
Step-by-step explanation:
15x3/4=45/4=11.25pounds
In ΔPQR, the measure of ∠R=90°, QP = 85, RQ = 13, and PR = 84. What ratio represents the cosecant of ∠P?
Answers
Given:
In ΔPQR, the measure of ∠R=90°, QP = 85, RQ = 13, and PR = 84.
To find:
The cosecant of ∠P.
Solution:
In a right angle triangle,
[tex]\text{cosec}\theta =\dfrac{Hypotenuse}{Perpendicular}[/tex]
It is also written as:
[tex]\text{cosec}\theta =\dfrac{Hypotenuse}{Opposite}[/tex]
In triangle PQR, QP is the hypotenuse because ∠R=90°.
[tex]\text{cosec}P =\dfrac{QP}{RQ}[/tex]
[tex]\text{cosec}P =\dfrac{85}{13}[/tex]
Therefore, the required trigonometric ratio is [tex]\text{cosec}P =\dfrac{85}{13}[/tex].
The number of students attending summer school at a local community college has been decreasing each year by 7%. If 847 students currently attend summer school at this rate continues, find the number of students attending summer school in 4 years.
Answers
Answer:
≈ 634
Step-by-step explanation:
n = 847(1 * .07)^4
n = 847(0.93)^4
n = 633.60005247
n ≈ 634
In how many ways can the letters A, C, E, G, K, S be arranged
Answers
Answer:720
Step-by-step explanation:Now let's imagine we are filling them with letters. There are six places we can put the first letter, so after we've placed one letter, we have six different outcomes.
There are then five remaining gaps for the second letter, so we have 5*6=30 different outcomes after two letters.
There are four spaces for the third letter, three for the fourth letter, two for the fifth letter and finally we have to put the sixth letter in the remaining gap.
So we end up with 6*5*4*3*2*1=720 ways to arrange six different letters.
This is called the factorial function, and is denoted by an exclamation mark. The factorial function is defined as the number of ways to arrange n different options and is calculated as n! = 1*2*3*…*(n-1)*n, with a extra bit that 0!=1 as there is one way to arrange a set of 0 objects (this comes into play later in statistics).